Recursion

A recursive function is a function that calls itself in its body, either directly or indirectly. Recursive functions have three important components:

1. Base case(s), the simplest possible form of the problem you're trying to solve.
2. Recursive case(s), where the function calls itself with a simpler argument as part of the computation.
3. Using the recursive calls to solve the full problem.

Let's look at the canonical example, factorial.

Factorial, denoted with the ! operator, is defined as:

n! = n * (n-1) * ... * 1

For example, 5! = 5 * 4 * 3 * 2 * 1 = 120

The recursive implementation for factorial is as follows:

def factorial(n):
    if n == 0:
        return 1
    return n * factorial(n - 1)

We know from its definition that 0! is 1. Since n == 0 is the smallest number we can compute the factorial of, we use it as our base case. The recursive step also follows from the definition of factorial, i.e., n! = n * (n-1)!.

The next few questions in lab will have you writing recursive functions. Here are some general tips:

• Paradoxically, to write a recursive function, you must assume that the function is fully functional before you finish writing it; this is called the recursive leap of faith.
• Consider how you can solve the current problem using the solution to a simpler version of the problem. The amount of work done in a recursive function can be deceptively little: remember to take the leap of faith and trust the recursion to solve the slightly smaller problem without worrying about how.
• Think about what the answer would be in the simplest possible case(s). These will be your base cases - the stopping points for your recursive calls. Make sure to consider the possibility that you're missing base cases (this is a common way recursive solutions fail).
• It may help to write an iterative version first.

Tree Recursion

A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.

A classic example of a tree recursion function is finding the nth Fibonacci number:

def fib(n):
    if n == 0 or n == 1:
        return n
    return fib(n - 1) + fib(n - 2)

Calling fib(6) results in the following call structure (where f is fib):

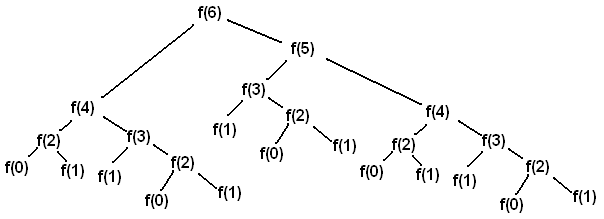
Each f(i) node represents a recursive call to fib. Each recursive call makes another two recursive calls. f(0) and f(1) do not make any recursive calls because they are the base cases of the function. Because of these base cases, we are able to terminate the recursion and beginning accumulating the values.

Generally, tree recursion is effective when you want to explore multiple possibilities or choices at a single step. In these types of problems, you make a recursive call for each choice or for a group of choices. Here are some examples:

• Given a list of paid tasks and a limited amount of time, which tasks should you choose to maximize your pay? This is actually a variation of the Knapsack problem, which focuses on finding some optimal combination of different items.
• Suppose you are lost in a maze and see several different paths. How do you find your way out? This is an example of path finding, and is tree recursive because at every step, you could have multiple directions to choose from that could lead out of the maze.
• Your dryer costs $2 per cycle and accepts all types of coins. How many different combinations of coins can you create to run the dryer? This is similar to the partitions problem from the textbook.

Lists

Lists are Python data structures that can store multiple values. Each value can be any type and can even be another list! A list is written as a comma separated list of expressions within square brackets:

>>> list_of_nums = [1, 2, 3, 4]
>>> list_of_bools = [True, True, False, False]
>>> nested_lists = [1, [2, 3], [4, [5]]]

Each element in a list is assigned an index. Lists are zero-indexed, meaning their indices start at 0 and increase in sequential order. To retrieve an element from a list, use list indexing:

>>> lst = [6, 5, 4, 3, 2, 1]
>>> lst[0]
6
>>> lst[3]
3

Often times we need to know how long a list is when we're working with it. To find the length of a list, call the function len on it:

>>> len([])
0
>>> len([2, 4, 6, 8, 10])
5

Tip: Recall that empty lists, [], are false-y values. Therefore, you can use an if statement like the following if you only want to do operations on non-empty lists:

if lst:
    # Do stuff with the elements of list

This is equivalent to:

if len(lst) > 0:
    # Do stuff

You can also create a copy of some portion of the list using list slicing. To slice a list, use this syntax: lst[<start index>:<end index>]. This expression evaluates to a new list containing the elements of lst starting at and including the element at <start index> up to but not including the element at end index.

>>> lst = [True, False, True, True, False]
>>> lst[1:4]
[False, True, True]
>>> lst[:3]  # Start index defaults to 0
[True, False, True]
>>> lst[3:]  # End index defaults to len(lst)
[True, False]
>>> lst[:]  # Creates a copy of the whole list
[True, False, True, True, False]